This post contains solutions to FiveThirtyEight’s two riddles released 2020-01-31, Riddler Express and Riddler Classic. Code for figures and solutions can be found on my github page.
Riddler Express
The riddle:
At the recent World Indoor Bowls Championships in Great Yarmouth, England, one of the rolls by Nick Brett went viral. Here it is in all its glory:12/10 on the mindblowing scale 🤯 #SCtop10
— SportsCenter (@SportsCenter) January 23, 2020
(via @BBCSport) pic.twitter.com/6pN6ybzVel
In order for Nick’s green bowl to split the two red bowls, he needed expert precision in both the speed of the roll and its final angle of approach.
Suppose you were standing in Nick’s shoes, and you wanted to split two of your opponent’s bowls. Let’s simplify the math a little, and say that each bowl is a sphere with a radius of 1. Let’s further suppose that your opponent’s two red bowls are separated by a distance of 3 — that is, the centers of the red bowls are separated by a distance of 5. Define ɸ as the angle between the path your bowl is on and the line connecting your opponent’s bowls. For example, here’s how you could split your opponent’s bowls when ɸ is 75°:
– Zach Wissner-Gross, "Can You Roll The Perfect Bowl? FiveThirtyEight
My Approach:
Sketched-out:
My drawings are rotated 90° clockwise from the problem description (does not affect solution)
Walked through:
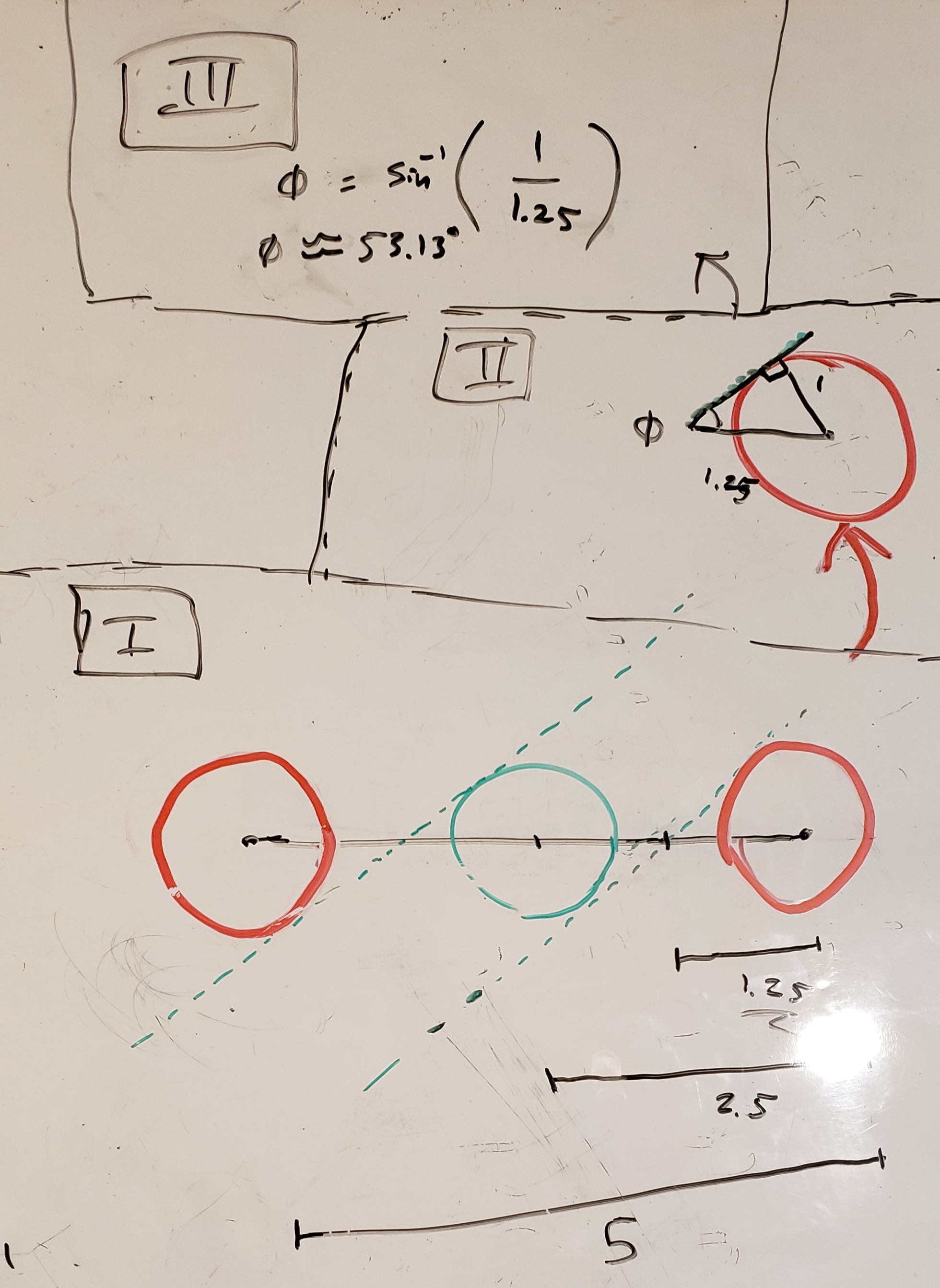
I. The minimum angle will be one where the green bowl touches points on both red bowls – this creates two tangents that you can think of as forming the track the green bowl travels down. Given the distance between the centers of the red bowls is 5 units, the distance between a green and a red bowl1 will be half this, 2.5 units. Also, the lines tangent to a red bowl and the green bowl will pass a point halfway between this at 1.25 units from the center of a red circle2.
II. Create the following three lines:
- Connect the centers of the red circles
- The line tangent to both a red circle and the green circle3
- The line perpendicular to the tangent point on the red circle
Connecting these lines will create a right triangle with side length of 1 and hypotenuse of 1.25.
III. If you remember the soh cah toa rules from trigonometry, you can use the identity \(sin(\phi) = \frac{opposite}{hypotenuse} \longrightarrow \phi = arcsin(\frac{1}{1.25})\) and compute the minimum angle is ~53.13°.
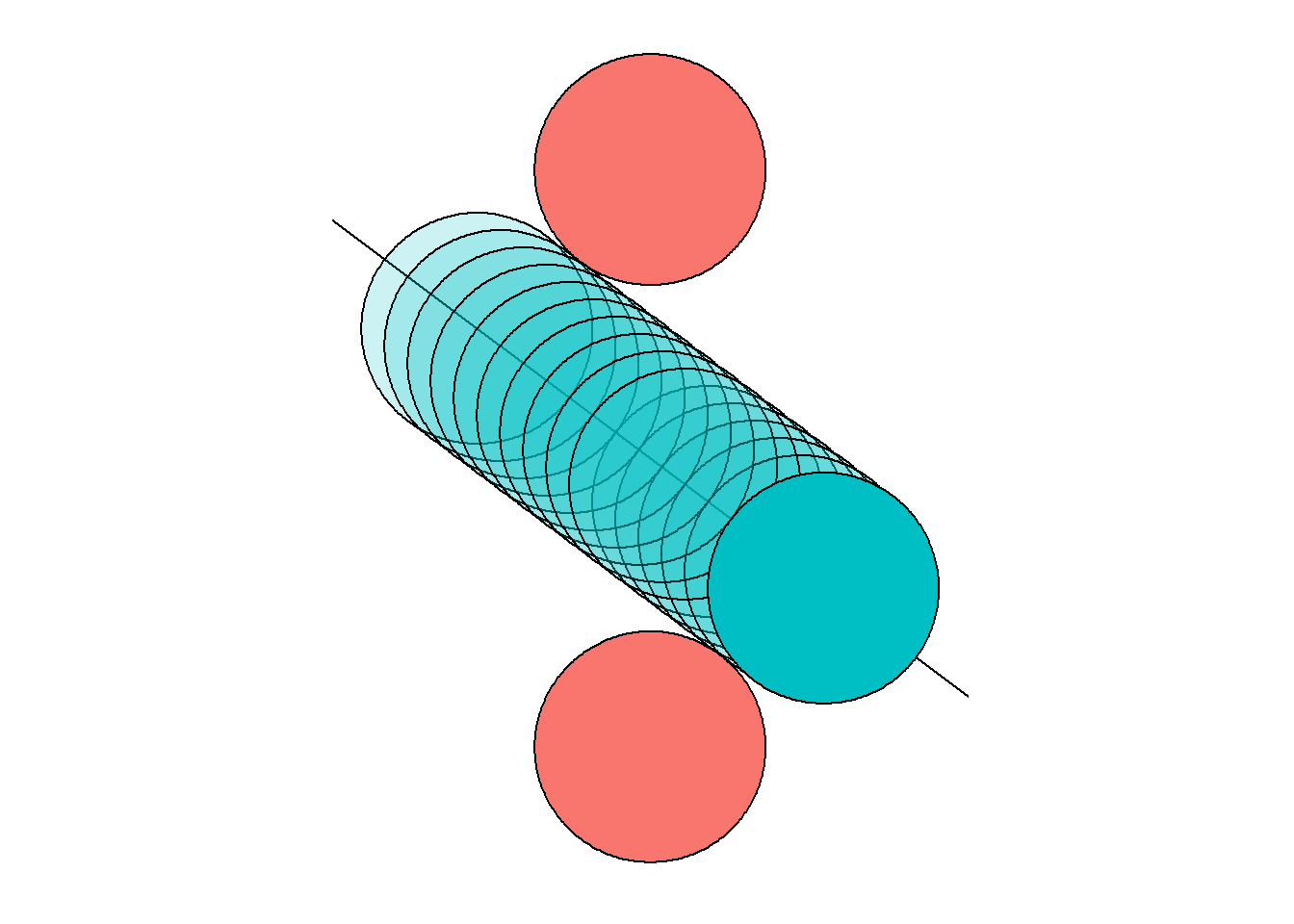
What the path of the perfect bowl would look like:
Riddler Classic
The riddle:
From Robert Berger comes a question of maximizing magnetic volume:
Robert’s daughter has a set of Magna-Tiles, which, as their name implies, are tiles with magnets on the edges that can be used to build various polygons and polyhedra. Some of the tiles are identical isosceles triangles with one 30 degree angle and two 75 degree angles. If you were to arrange 12 of these tiles with their 30 degree angles in the center, they would lay flat and form a regular dodecagon. If you were to put fewer (between three and 11) of those tiles together in a similar way, they would form a pyramid whose base is a regular polygon. Robert has graciously provided a photo of the resulting pyramids when three and 11 tiles are used:
– Zach Wissner-Gross, "Can You Roll The Perfect Bowl? FiveThirtyEight
My Approach:
The Magna-Tiles will form regular pyramids. The question is which n-sided pyramid will have the greatest volume. \[(Volume\;of\;a\;pyramid) = \frac{1}{3}(area\;of\;base)(height\;of\;pyramid)\] Hence we need to first calculate the Area of the base of the pyramid and the Height of the pyramid. I’ll set-up a way of calculating these as a function of the number of (75°-75°-30°) Magna-Tiles.
Area of the base of the pyramid
The side length of the base of our pyramid will be the length of the shortest side of a Magna-Tile. We weren’t told the lengths of the sides of the Magna-Tiles but they don’t matter for this problem4. To keep things simple, I’ll say the two congruent sides of the Magna-Tiles are equal to 1 unit.
Drawing a line perpendicular to the base splits our Magna-Tile into two congruent triangles. Given the trigonometric identity that \(sin(\theta) = \frac{opposite}{hypotenuse}\) and that the hypotenuse of each triangle was set at 1 unit, we can calculate the length of the base of the Magna-Tile is 2sin(15°).
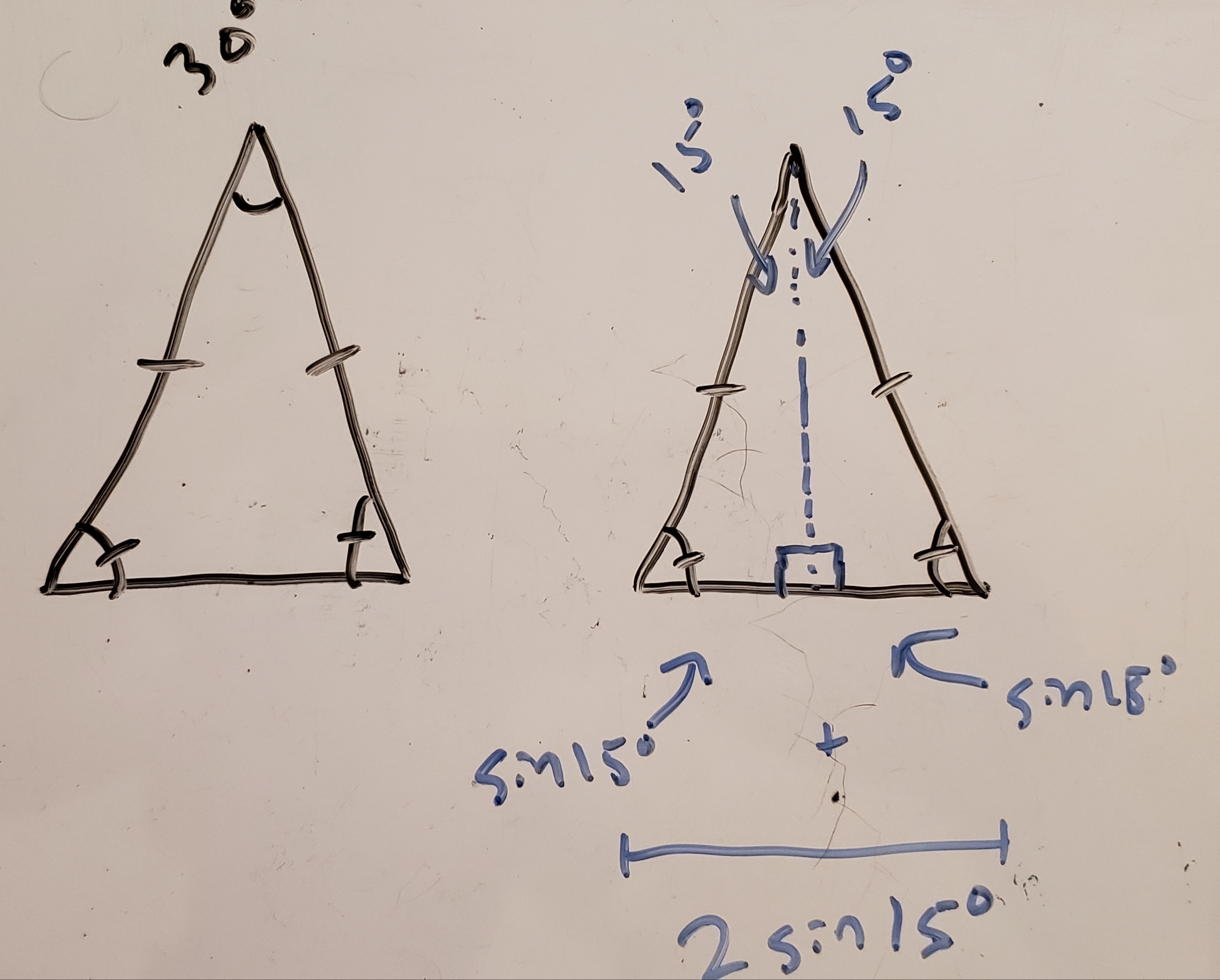
Base polygon side length
I used Math Open Reference to find an equation for area of a regular polygon as a function of side length and number of sides: \[(area\;of\;regular\;polygon)\;=\;\frac{(side\;length)^{2}(number\;of\;sides)}{4tan(\frac{180^{\circ}}{number\;of\;sides})}\]
You can replace (side length) in this equation with 2sin(15°) (calculated above), making area a function of only the number of sides on our pyramid (i.e. the number of Magna-Tiles).
Height of the pyramid
Sketched out:

Finding pyramid height
Walked through:
The highest point of the pyramid will rest over the center of the base polygon. You can imagine a right triangle on the interior of a regular n-sided pyramid with its three line segments corresponding with:
I. the length of a Magna-Tile (over its line of symmetry)
II. an apothem of the pyramid’s base (an apothem is just a line segment from the center of a regular polygon to the middle of any side)
III. the pyramid’s height
Calculating I & II will enable us to use the Pythagorean Theorem to calculate the pyramid height.
I. Length of a Magna-Tile (over its line of symmetry)
Using the trigonometric rule that \(cos(\theta) = \frac{adjacent}{hypotenuse}\) reveals the length of a Magna-Tile as equal to cos(15°) – remember we are treating the longest sides of the Magna-Tile as equal to 1 unit5.
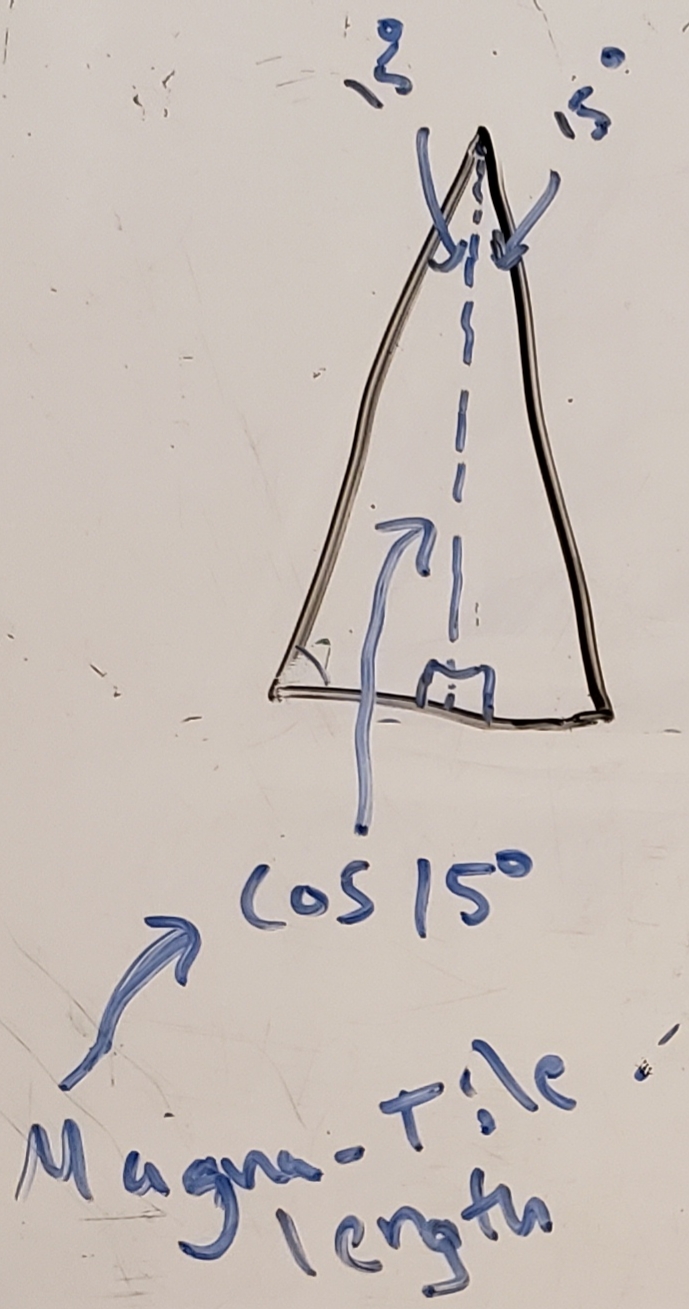
Magna-Tile length (over its line of symmetry)
II. I used Math Open Reference to find the equation for apothem length as a function of number and length of sides in a regular polygon. \[apothem\;length = \frac{side\;length}{2tan(\frac{180^{\circ}}{number\;of\;sides})}\] You can replace side length in this equation with 2sin(15°) (calculated above), making apothem length a function of only the number of sides on our pyramid (i.e. the number of Magna-Tiles).
III. Parts I and II represent two sides of a right triangle. To find the third side (corresponding with pyramid height) simply use the Pythagorean theorem: \[pyramid\;height = \sqrt{(MagnaTile\;length)^{2} - (apothem\;length)^{2}}\] Fill in the values for (Magna-Tile length) and (apothem length) (as described in I & II) and you’ll see pyramid height is now represented as a function of only number of sides (i.e. number of Magna-Tiles).

Finding pyramid height
Encode functions and calculate volumes
I used R to encode these functions6 and calculate the volumes for pyramids built from 2 to 12 Magna-Tiles7.
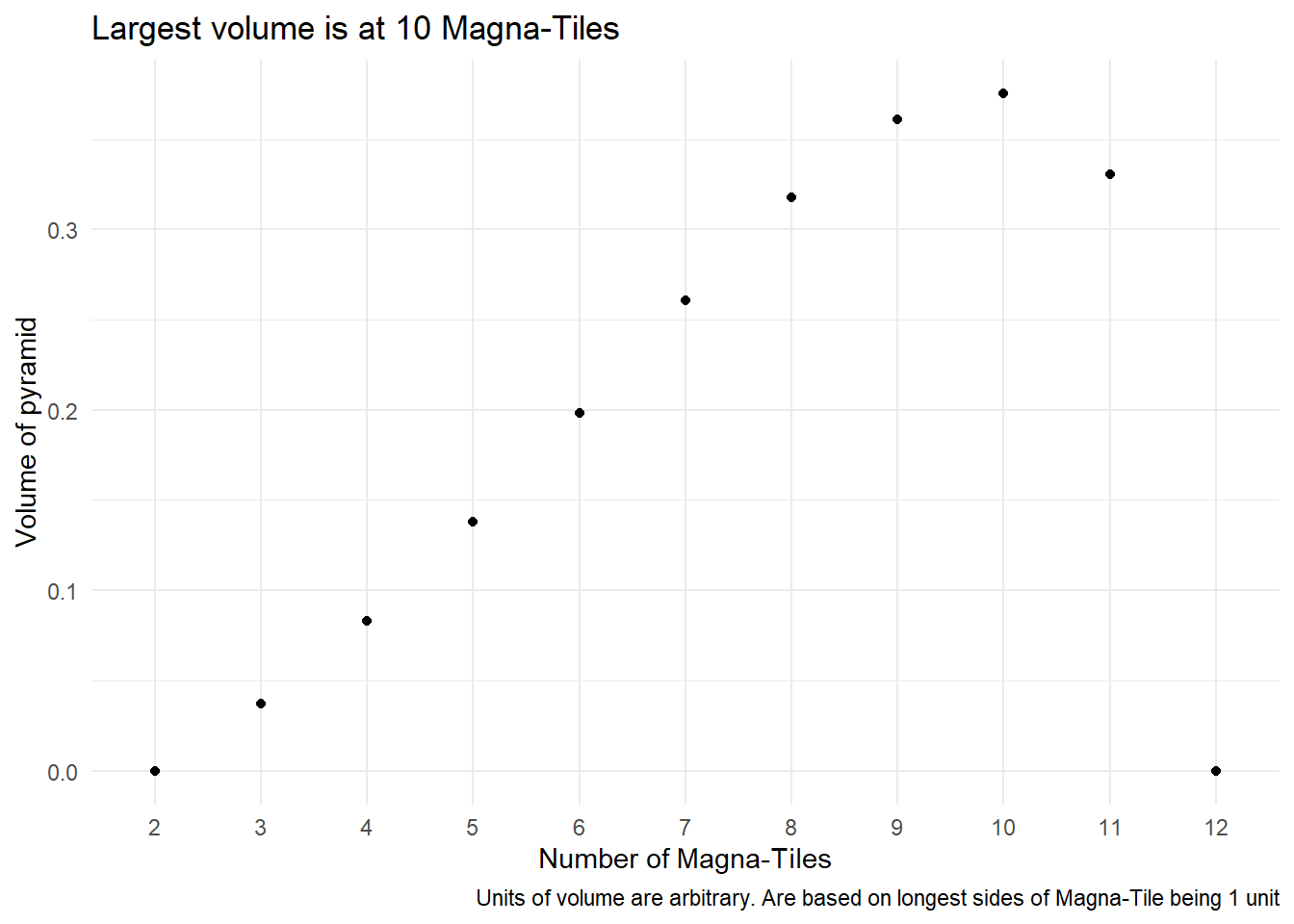
- Volume increases up until 10 Magna-Tiles and then decreases at 118.
Appendix
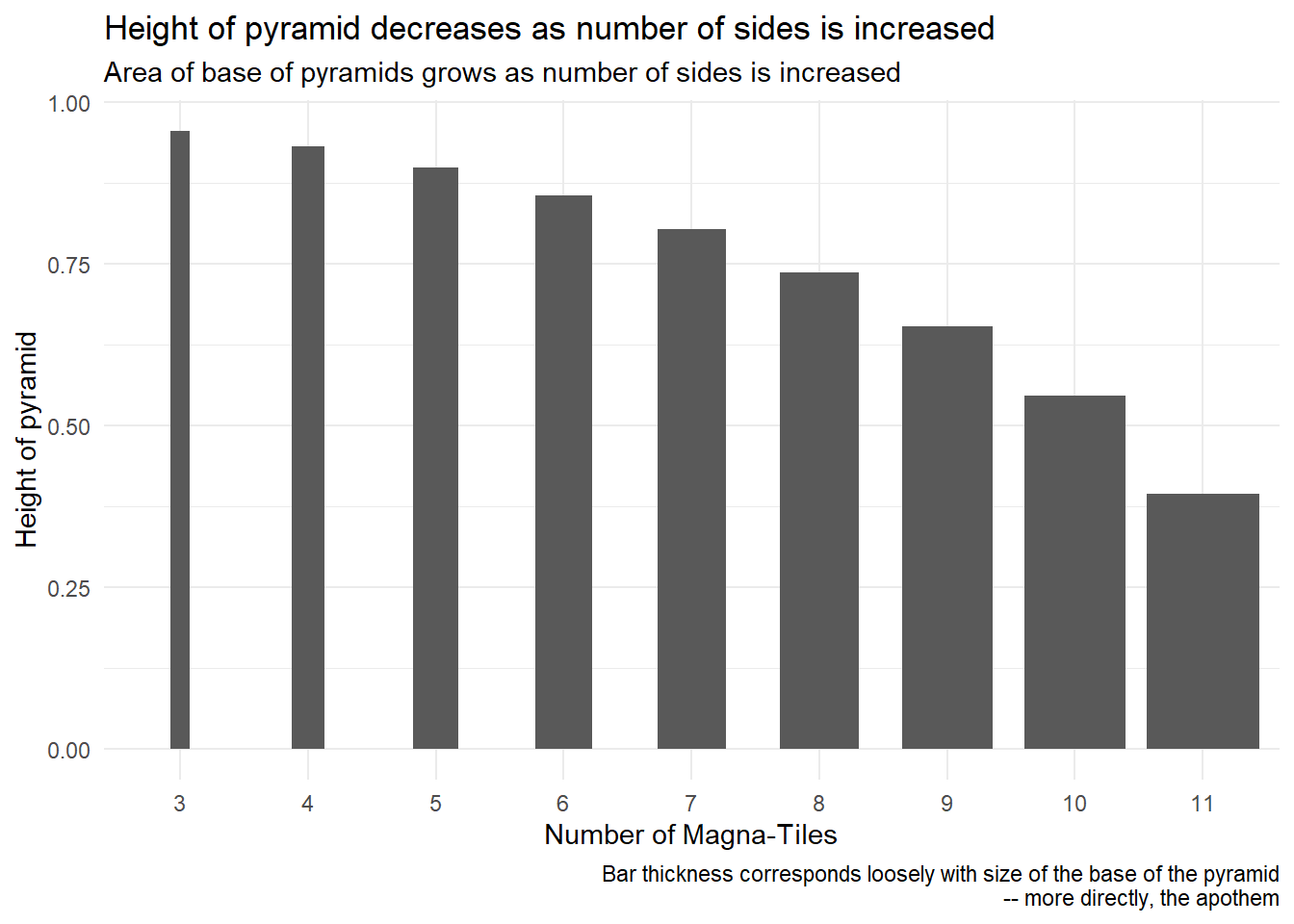
Bonus plot showing number of tiles (and size of pyramid base) vs pyramid height.
When passing the line between the centers of the red circles.↩︎
When passing the line between the centers of the red circles.↩︎
Could do for either or both circles and would get same solution as below steps will form congruent triangles – but following these steps using the top red circle more closely follows the story of the problem.↩︎
As the pyramids created will be similar so each pyramid would scale proportionally to one another.↩︎
In this case the longest sides are each a hypotenuse.↩︎
In the code I use pi / 12 radians, which is equivalent to 15° used throughout the descriptions.↩︎
2 and 12 Magna-Tiles represent flat structures ad therefore no volume.↩︎
At 12 the structure is flat so no longer has volume.↩︎

